Ⅰ. 서론(목적)
RLC 회로의 구성과 각 구성요소의 역할, 임피던스의 개념을 이해할 수 있다.
Ⅱ. 이론적 배경
저항(R, Resistance)은 도체에서 전류의 흐름을 방해하는 정도를 나타내는 물리량이다. 옴의 법칙에 따라,

이라는 전압과 전류 사이의 관계를 갖는다.
I=I_0 cos(wt)라고 하면, V=I_0 cos(wt) 가 된다.
코일(L, Inductance)은 인덕턴스를 가진 전선을 감은 꼴의 수동소자이다. 코일의 전압은 다음과 같은 관계를 갖는다.

I=I_0 cos(wt) 라고 하면 V_L=-wLI_0 sin(wt) = wLI_0 cos(wt+pi/2)가 된다. 코일의 전압은 저항의 전압과 달리 걸어준 전류의 각진동수에 비례하고 위상차가 존재함을 알 수 있다.
축전기(C, Capcitance)는 전기 회로에서 전기용량을 전기적 퍼텐셜 에너지로 저장하는 장치이다. 도체판 한쪽에 모이는 전하의 양을 Q라고 하며 다음의 관계를 갖는다.

'전류의 정의는 시간에 따른 전하량의 변화이므로, 식을 적분으로 나타내어 정리할 수 있다'라고 할 때,

가 된다. 코일의 전압과 달리 축전기의 전압은 걸린 전류의 각진동수에 반비례하고 위상차가 존재함을 알 수 있다.
RL회로는 저항과 코일로 이루어진 회로이다. RL회로에 키르히호프의 고리 법칙을 시계 방향으로 적용하면,

ε 는 전지의 기전력(전체 회로에 걸리는 전압)이다. 양변을 R로 나누고 x= ε /R - I로 치환하면,

변수 분리하여 적분하면,
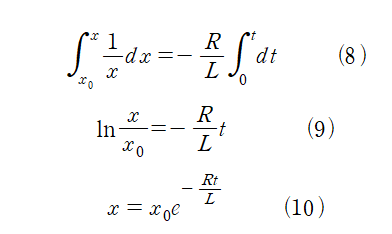
x_0는 t=0일 때의 x이고, t=0일 때 I=0이므로 x_0= ε /R이다.
따라서,

상수 τ 는 회로의 시간 상수로 τ = L/R이다.

저항의 전압과 전류의 위상은 동일하고, 코일의 전압은 전류와 pi/2 만큼의 위상차이가 난다.(코일의 전압의 위상이 pi/2만큼 전류보다 빠르다) 따라서 전체 전압과 전류 사이의 위상차는 θ = cos^(-1)(V_R/V) 로 구할 수 있으며 θ 만큼의 위상차이가 남을 알 수 있다.
RC회로는 축전기와 코일로 이루어진 회로이다. RL회로와 동일하게 전체 회로에 걸린 전압에 대한 식을 세울 수 있다.

I=dQ/dt이므로,
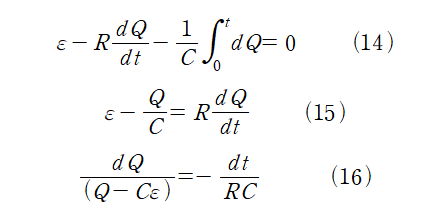
양변에 t=0부터, t까지 적분을 취하면,
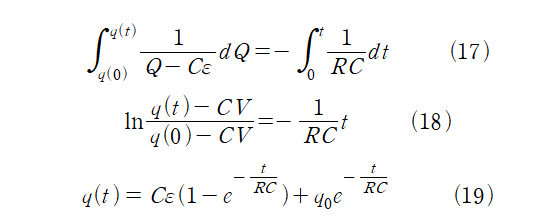
t=0일 때의 축전기의 전하량은 0이므로 q(0)=0이다.
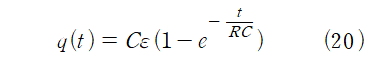
양변을 시간에 대해 미분하면, 전류에 관한 식으로 정리할 수 있다.
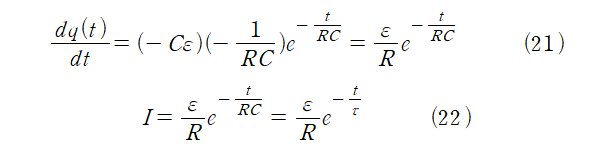
RC회로의 시간 상수 τ 는 τ =RC이다.

저항의 전압과 전류의 위상은 동일하고, 축전기의 전압은 전류와 pi/2만큼의 위상차이가 난다.(코일의 전압의 위상이 pi/2만큼 전류보다 느리다) 따라서 전체 전압과 전류 사이의 위상차는 θ = cos^(-1)(V_R/V) 로 구할 수 있으며 θ 만큼의 위상차이가 남을 알 수 있다.
LC회로는 코일과 축전기로 이루어진 회로이다. 초기 상태에서 축전기의 최대 전하를 Q_max라 하면 축전기에 저장된 전체 전기 에너지는 (Q_max)^2/(2C)이다. 전기에너지가 코일의 자기에너지로 모두 저장되기 이전에 중간 지점에서의 에너지 일부는 전기 에너지이고, 일부는 자기 에너지이다.
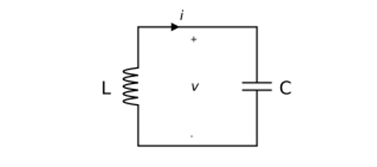

회로 내부 저항이 없고, 전자기적인 복사가 없다고 가정할 때, 에너지가 내부 에너지로 전환되지도 않고 회로의 계 외부로 유출되지도 않으므로 계의 전체 에너지는 시간에 무관한 상수 값을 갖는다.
즉, dU/dt=0 이므로.

i=dq/dt이므로,

단조화 운동하는 입자의 운동 방정식
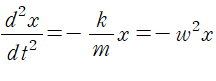
와 동일한 형태임을 알 수 있다.
w=1/(LC)^(1/2)일 때,
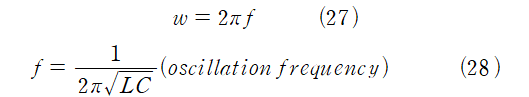
단조화 운동하는 입자의 운동 방정식의 일반해와 동일한 형태의 일반해를 가지므로,
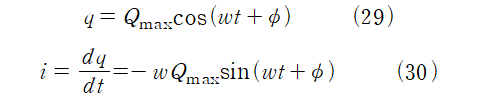
t=0, i=0, q=Q_max 로 가정하였으므로 위상각 φ 는 φ =0이다.
따라서,
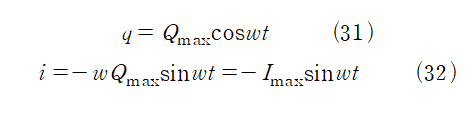
RLC회로는 저항, 코일, 축전기로 이루어진 회로이다. RL, RC회로와 동일하게 다음과 같이 나타낼 수 있다.
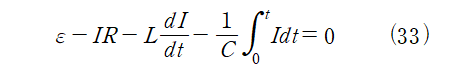
I=I_0 cos(wt)라고 할 때,

(1/(wc)-wL)^(2)=0이 될 때, Z는 최소가 되고 I는 최대가 된다. 이때의 각진동수 w는 w=1/(LC)^(1/2)가 된다.
이 때의 주파수
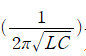
를 RLC회로의 공명 주파수라고 한다.
Ⅲ. 실험 방법
1. 실험 준비물
파스코 RLC 회로, 신호 발생기를 포함하는 인터페이스, 센서, 접지선, 신호선
2. 실험 방법
가. RL회로
1) 각각 저항의 아래쪽 단자에 접지선을 연결하고 다른 신호선(+극) 코일의 오른쪽 단자에 연결한다.
2) 전압센서를 A,B 포트에 각각 저항과 코일을 연결해준다. 전압 센서의 접지선과 회로의 접지선이 가깝도록 연결해주고 (+)극 선은 그와 멀도록 각각 연결한다.
3) Pasco Capstone 프로그램을 연 후, 인터페이스의 각 포트의 센서를 설정하고 신호 발생기를 켠다.
4) 신호 발생기 설정 탭에서 신호의 주파수와 파형, 전압, 진폭을 설정할 수 있다.
5) 각각의 전압을 시간에 따라 측정하여 위상차, 전압, 임피던스를 분석한다.
나. RC회로
1) 각각 저항의 아래쪽 단자에 접지선을 연결하고 다른 신호선(+극) 축전기의 아래쪽 단자에 연결한다.
2) jumper line을 코일의 양쪽 단자에 연결한다.
3) 전압센서를 A,B 포트에 각각 저항과 축전기를 연결해준다. 전압 센서의 접지선과 회로의 접지선이 가깝도록 연결해주고 (+)극 선은 그와 멀도록 각각 연결한다.
4) Pasco Capstone 프로그램을 연 후, 인터페이스의 각 포트의 센서를 설정하고 신호 발생기를 켠다.
5) 신호 발생기 설정 탭에서 신호의 주파수와 파형, 전압, 진폭을 설정할 수 있다.
6) 각각의 전압을 시간에 따라 측정하여 위상차, 전압, 임피던스를 분석한다.
다. RLC회로
1) 회로의 양 끝단(저항의 아래쪽 단자와 축전기의 아래쪽 단자)에 접지선과 신호선을 연결한다.
2) 전압센서를 A,B,C 포트에 각각 저항, 코일, 축전기를 연결한다. 전압 센서의 접지선과 회로의 접지선이 가깝도록 연결한다.
3) Pasco Capstone 프로그램을 연 후, 인터페이스의 각 포트의 센서를 설정하고 신호 발생기를 켠다.
4) 신호 발생기 설정 탭에서 신호의 주파수와 파형, 전압, 진폭을 설정할 수 있다.
5) 각각의 전압을 시간에 따라 측정하여 위상차, 전압, 임피던스를 분석한다.
Ⅳ. 결과 분석 방법
1. RL 회로
저항에 따른 t-V_0, t-I_0, t-V_R 그래프를 각각 그린다. 그래프 상에서 V_0와 I_0의 위상차와 V_R과 V_L의 위상차를 계산할 수 있다
w를 구하고 임피던스 Z를 계산할 수 있다.
2. RLC회로
저항에 따른 t-V_R, t-V_L, t-V_0, t-I_0 그래프를 각각 그린다. 그래프 상에서 V_0와 I_0의 위상차, V_R과 V_L사이의 위상차, V_R과 V_C의 위상차를 계산할 수 있다.
w를 구하고 임피던스 Z를 계산할 수 있다.
'과학&공학 > 일반물리학실험' 카테고리의 다른 글
| [일반물리학 실험 #10] 지구 자기장 측정 (Measuring the Magnetic Field of the Earth) (2) | 2024.07.24 |
|---|---|
| [일반물리학 실험 #09] 패러데이 유도 법칙 (Faraday Induction Law) (1) | 2024.06.28 |
| [일반물리학 실험 #07] 열기관 순환 (Heat Engine Cycle) (0) | 2024.04.28 |
| [일반물리학 실험 #06] 공명관 실험(Resonance Tube) (0) | 2024.04.02 |
| [일반물리학실험 #05] 회전관성 (Moment of Inertia) (0) | 2023.05.17 |




댓글