Ⅰ. 서론(목적)
패러데이의 전자기 유도 법칙에서 면적이 달라짐에 따른 유도 기전력의 변화를 이해하고 이를 이용하여 지구의 자기장을 측정할 수 있다.
Ⅱ. 이론적 배경
패러데이의 전자기 유도 법칙은 N번 감긴 코일에 대하여 다음과 같이 기술할 수 있고 Φ_B = vector(B) ⋅ vector(S)이다. U는 유도 기전력, vector(B)는 자기장, vector(S)는 표면에 대한 법선벡터이다,

만약 물체가 z축에 대하여 w만큼의 각속도로 회전하고 있다면 표면에 대한 법선벡터 vector(S)는,

이 실험은 회전에 의해 면적만 변하는 경우이므로, z축에 대하여 회전할 때 발생하는 유도 기전력 U_z는 다음과 같이 나타낼 수 있다.

동일한 방법으로 각각 x, y, z축에 대하여 회전할 때, 유도 기전력은

유도 기전력에서 사인함수를 제외한 진폭에 해당하는 부분은 다음과 같다.
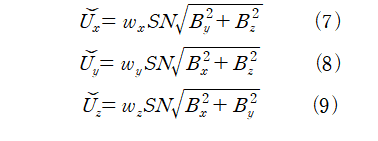
w_x = w_y = w_z = w 인 경우 B_x, B_y, B_z에 대해 다음과 같이 나타낼 수 있다.

복각은 다음의 관계를 이용하여 구할 수 있다.

코일의 회전을 통해 면적을 변화시키면서 각각의 회전축에 대한 유도 기전력을 측정하여 각각의 축에 대한 지구 자기장의 크기 정보를 얻을 수 있다. 지구의 자기장은 일정한 방향과 크기로 존재하나 각 방향에 대한 면적이 변화함에 따라 코일을 지나는 자기 선속이 변하므로, 유도 기전력이 발생한다. 유도 기전력의 최댓값을 이용하여 최대면적, 감은 수, 자기장, 각속도에 대한 정보를 얻을 수 있으므로, 코일의 최대면적과 감은 수, 각속도를 알고 있다면 자기장의 크기를 계산할 수 있다. 이 과정을 통해 각 축에 대한 지구 자기장의 값을 계산하여, 지구 자기장과 지면(수평면)에 대해 지구 자기장이 기울어진 정도인 복각을 구할 수 있다.
Ⅲ. 실험 방법
1. 실험 준비물
320번 감은 코일, 회전 모터, 인터페이스, 전압 센서, 회전 방향과 각 속도를 조정할 수 있는 모터 조종기
2. 실험 방법
(1) 코일의 양쪽 끝을 전선으로 연결하여 전압 센서의 , 극으로 연결한다.
(2) 전압 센서를 인터페이스에 연결하고 인터페이스를 컴퓨터에 연결한다.
(3) 코일을 회전 모터에 연결하고 모터 조종기를 이용하여 각속도와 회전 방향을 조절할 수 있다.
(4) 한 축에 대하여 코일을 회전시키면, 그 축에 대해서는 유효 면적이 0에 가깝고 변하지 않으므로 다른 두 축의 성분에 해당하는 자기장에 의해서만 유도 기전력이 발생하므로, 각 축에 대하여 모두 실험을 진행한다.
(5) 정해진 각속도로 축에 대하여 코일을 회전시키면서 발생한 유도 기전력을 측정한다.
(6) 축에 대해서도 같은 과정을 수행한다.
(7) 전압 센서를 통해 얻어낸 값으로 그래프를 그려, 진폭의 크기와 주기를 분석한다.
(8) 각 축에 대하여 자기장의 크기를 분석하고, 복각을 구한다.
3. 실험 가정
코일이 수백 번 이상 감겨 있는 경우 도선의 두께로 인하여 코일의 두께를 고려해야 한다. 코일의 안쪽 반지름을 R_1 , 바깥쪽 반지름을 R_2라고 할 때, 두께와 감은 수에 관한 식을 다음과 같이 나타낼 수 있다.

자기 선속이 코일의 안쪽에서 발생한다고 가정하면 자기 선속 Φ_B는,

코일의 두께가 코일의 반지름에 비해 충분히 작은 경우, R_1 R_2이므로,

으로 나타낼 수 있고, 자기 선속을 하나의 반지름으로 나타낼 수 있으므로 코일의 두께가 유효한 차이를 나타내지 않음을 알 수 있다.
Ⅳ. 결과 분석 방법
x 축, y축, z축에 대하여 코일을 회전시킬 때, 시간에 따른 유도 기전력 그래프를 그린다.
코일의 안쪽 반지름의 면적이 자기 선속이 지나는 면적으로 가정한다.
T= 2pi/w와 식(10), (11), (12)를 이용하여 각각의 축에 해당하는 자기장의 크기를 구한다.
각 축 별 자기장의 크기를 통해 B를 구하고 대한민국에서의 지구 자기장의 크기와 비교하여 오차율을 계산한다. 식(13)을 이용하여 복각도 계산하여 실제 대한민국에서의 복각과 오차율을 계산한다.
코일의 안쪽 반지름과 바깥쪽 반지름의 평균에 의한 면적이 자기 선속이 지나는 면적으로 가정하고 동일한 과정을 수행하여 오차율을 계산한다.
'과학&공학 > 일반물리학실험' 카테고리의 다른 글
| [일반물리학 실험 #09] 패러데이 유도 법칙 (Faraday Induction Law) (1) | 2024.06.28 |
|---|---|
| [일반물리학 실험 #08] RLC 회로 (RLC Circuits) (0) | 2024.06.27 |
| [일반물리학 실험 #07] 열기관 순환 (Heat Engine Cycle) (0) | 2024.04.28 |
| [일반물리학 실험 #06] 공명관 실험(Resonance Tube) (0) | 2024.04.02 |
| [일반물리학실험 #05] 회전관성 (Moment of Inertia) (0) | 2023.05.17 |




댓글